Creating Phyllotaxis
The Stack-and-Drag Model
Frank
M. J. van der Linden
[2007]
|
|
PhaseLab
Foundation |
|
address |
Binnewiertzstraat 15 5615 HE Eindhoven The Netherlands |
|
phone |
+31 0625027054 |
|
email |
|
|
web |
from the original publication, printed in B&W, in
MATHEMATICAL BIOSCIENCES 133:21-50 (1996)
by Elsevier, NY SSDI 0025-5564(95)00077-Q
Abstract
The genesis of phyllotaxis, the origin
of the pattern of appendages on the surface just below the apical extreme of
many plants, is an old unsolved puzzle. Whereas many models generate helices,
the stack-and-drag model is the first to achieve this in an integral
construction from seed to flower. Combination of the principle of gnomonic
growth, where consecutive additions have comparable positions, with a
"dragging" principle, where the developing zone follows the apical
tip, provides a powerful tool in simulating a wide range of phyllotactic
manifestations. The influence of three vital parameters for primordial size,
compressibility, and canalization (or annular arrangement) helps in
understanding the problem's nature.
1 Introduction
1.1 Observed
patterns and some divergent models
Most plant bodies
show a radial symmetry as a consequence of their axial development. Primordia
(early appendages) are ordered in various phyllotactic patterns such as
distichous (or opposite), decussate (or cross-opposite), in whorls, or in
parastichies (or spirals and helices). Therefore it seems defendable to start a
simulation for pattern generation from a centric growth principle.
Investigations on pattern formation of epidermal cells in vegetative ontogeny
[1-3], centric experiments [4], and centric surface models [5-8] show that use
of (centric) surface models can be practical. However, studies on floral
ontogeny [9, 10] and surgical experiments [11, 12] clearly contradict a purely
centric theory by showing that centric phyllotaxis can be deduced from (or
influenced after) peripheral pattern formation.
1.2 Differences
from other models
This paper presents
a phyllotactic model of which the spheres close-packing or stacking principle
is traditional to some degree [13-15] but employs a dragging principle where
primordium stacking below certain regions is prohibited. The use of a dragging
aspect as a counterpart of gravity and adhesion is justifiable, for new
material arises continuously at the top of the stem whereas the epidermal and
lower layers have to follow. In the model, this dragging causes canalization of
organ numbers or the tendency of organ numbers to remain constant in spite of
genetic or environmental variation [16]. Canalization has not previously been
incorporated in phyllotactic models for complete plant bodies. The arrangement
of primordia in concentric circles on the shoot apex is also responsible for
the annular differentiation of flower parts [17].
In contrast to
existing theories that are based on observed geometrical consequences (like the
Fibonacci angle of 137.5¡) [13-15, 18-30], the stack-and-drag model uses the
gnomonic growth property [31], which makes the introduction of distances or
angles to control correct unit positioning redundant. (For an understanding of
the mechanism used in the construction of primordial units in the
stack-and-drag model, a knowledge of the algorithms in the dislodgement model
[7] is necessary. A structure grows gnomonically if it keeps its form during
the process. An example is shown by the snail, which grows its shell by secreting
ever larger amounts of chitin on the open side of the helical tube [32]. A more
basic example is the planar stacking of growing circles from a center outward.
Every circle is constructed against its predecessor in the same rotation
direction around the initial circles. The result is a simple spiral of circles
of increasing size. The dislodgement model [7, 33] obeys a slightly more
complicated mechanism. Every new circle is initially constructed in a
consequent position in relation to its predecessor. The structure's disk shape
is maintained by adjusting configurations when a neighboring circle should
intersect the new one. The stack-and-drag model resembles the dislodgement
model, but has more biological justification because it shows (1) a stacking
from base to top, (2) a predefined transition vegetative-generative stage, and
(3) restricted settling of primordia in a zone.)
1.3 Goals
and limitations of the theory
To demarcate the
field of study, ramifications [34] are excluded. The model strives for
(1) Continuity in
development from cotyledons to inflorescences and flowers (any initiating rule
is consequently repeated from the very start, regardless of the motive behind
it)
(2) A very limited
set of easily recognizable parameters frequently mentioned in the literature
(3) Numerical and
graphical output that can easily be compared with observations reported in the
literature [19, 35, 36]
(4) Solutions of
some open problems in phyllotaxis [35, 37-39]
(5) Consistency,
according to recommendations for phyllotaxis theories [39].
2 Approach
and biological evidence
2.1 Cotyledons,
stem, and flowering
The stack-and-drag
model follows a tradition in the geometry of close-packing of spheres or
circles in nonliving structures [40-42]. (Filling surfaces and bodies with
circles and spheres has a long tradition that can be traced back to Plato,
Archimedes, Kepler, and Kelvin.) The stacking is from two initial similar and
touching spheres, like cotyledons, upwards. A phyllotactic unit is defined as a
primordium or a sphere of influence including the
"primordium"-forming cells. Primordial units may be shaped as spheres
and arise one after the other with a nearly constant time interval
(plastochron). The vegetative stem (Figure 1) is presented as an infinite
cylinder (Figure 2).
The switch from vegetative to
generative growth (flowering) [17] (Figure 3) is simulated by ending the
cylinder stacking. Now, an apical hemisphere with radius 1 becomes the bearer
of primordial spheres of constant radii [16] (Figure 4). For flower heads, the
distance ratio becomes relatively small just before flowering, and units are
nearly constant in size. In simulations of vegetative structures and flowers,
units will soon fill up the hemisphere.
2.2 The
gnomonic principle: biological justification and application in the model
In investigations
and modeling in phyllotaxis, primordia are identified by numbering them in a
logical way [37]. In general, it is an open question as to whether the numbers
represent the actuaI succession of inception or not [16], but it is often seen
that successively numbered, primordia are embedded in similar regions, in other
words, subsequently arising primordia lean against subsequent
environments. This empirical rule is equivalent to the rule that a
plant grows gnomonically. Any primordium has generally the same difference in
ordinal order or age from its lower contacts as the preceding primordium had
from it. This holds for all primordia. Small positional and dimensional
adjustments are of second order. In floral plant structures the gnomonical way
of growing is not obvious. However, phyllotactic pattern generation takes place
in early stages in plant development, while primordia are not differentiated
and the apical dome keeps its form more or less [20], so there is gnomonical
growth.
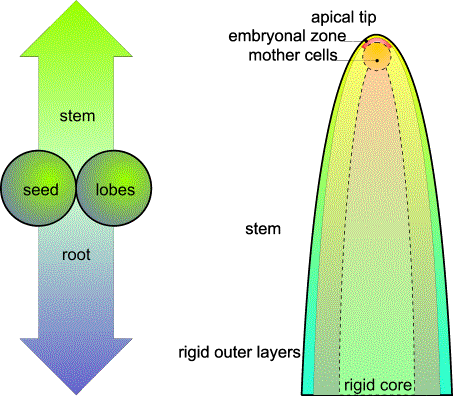
FIG.1. The origins of vegetative phyllotaxis. Left: Basically, dicotyledons show horizontal and vertical symmetry. Only
dicotyledons, and only the shoot, are the subject of study. Right: Just below the extreme top, a cluster of cells with an active envelope
is continuously pushed forward by the elongating and multiplying shoot cells.
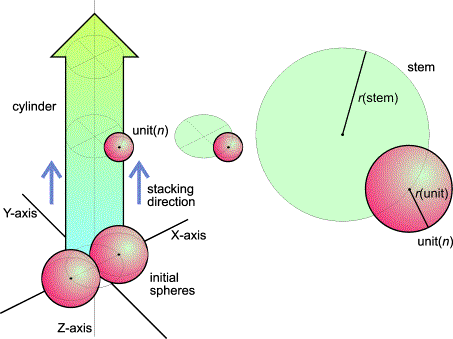
FlG.2. The stack-and-drag model: initiation (left) and relation r(unit)/r(stem) in the vegetative stage.
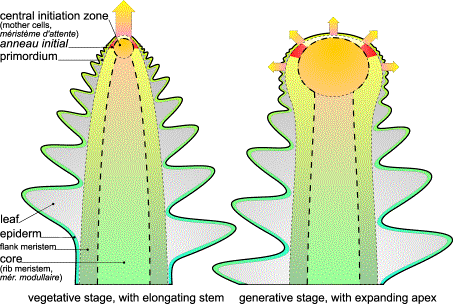
FIG.3. Growth directions in vegetative and generative stages. Left: The mother cells are pushed upward, thereby dragging their mitotic
active envelope, which is annular [43]. The very top is quiet and does not
generate primordia. Right: While the apical
dome expands, reproductive organs are generated. In flower heads, as shown, the active ring remains behind for some time
before it rapidly closes on the top while primordia arise as little hemispheres
on the surface.
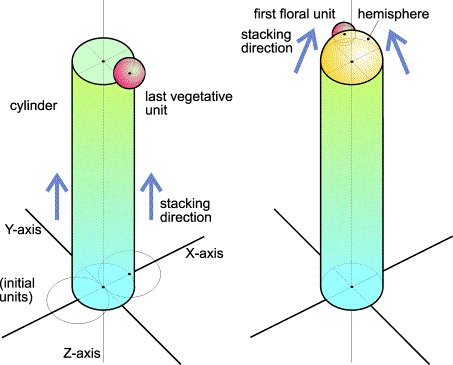
FlG.4. The stack-and-drag model: from vegetative (left) to generative stage.
In the plant, the inception of a new
primordium is a local event that depends on certain circumstances such as
gravitation, surface tension, expansion, and chemical influences. More
important here is the ascertainment that (1) circumstances are broadly stable
in time and (2) heredity plays a modest part. (Phyllotaxis shows an important
phenomenon. Different species may show the same phyllotaxis, and within a
species or even an individual plant, different but stable phyllotactic patterns
are possible. This indicates a geometric constraint to have dominance over
differentiation-determining forces. An example of species overriding geometry
is the ubiquity of Fibonacci numbers with typical anomalies like the Lucas
numbers. In cases where phyllotaxis is unstable, the geometric constraint may
be subsidiary to genetic or environmental variations.) In order to predict the
site at which a new unit will arise, the stack-and-drag model makes use of the
gnomonic growth principle. In other words, the place of a new unit in a
configuration at a certain point in time tells much about the place in which
the next unit will arise (Figure 5). By applying the gnomonic property,
modeling is possible without the instant need of knowledge of underlying
mechanisms. The stack-and-drag model can be said to include other models in the sense that it neither follows any of three well-known
hypotheses, nor excludes them:
(1) New primordia
should arise as far as possible from newly born primordia [14, 27, 44], which
implies an inhibitor mechanism. Many phyllotactic patterns seem to obey this
theory, but others, such as the monostichous spiral, contradict it [35].
(2) New primordia
should arise at the first available space [45], which implies a tension field
theory.
(3) A new
primordium is positioned by mechanical pressure of its contacts [18, 46]. This
does not account for the initiating location of a new primordium.

FIG.5. At time t+1 a new primordium will
become visible, but where? In looking back at the structure at time t, we see that the new primordium there arose between or against two support
units of which we know the ordinal numbers p and q (see Figure 8). Because, when turned,
structure t+1 fits on structure t, the new primordium will arise in neighborhood t+1. Thus, at time t+1, we choose support
units with an age of one plastochron younger (or with ordinal numbers p+1 and q+1) than the support units
of the primordium that just arose. If positioning is impossible for any reason,
we have to shift the new unit (see Section 3.1).
2.3 Separation
of pattern formation and structural growth
During formation of phyllotactic
patterns, the plant is growing. In the model, pattern generation is separated
from structural expansion. The geometric relationships between neighboring
units and stem radius just at the inception of a new unit form the
basis for the consequently arising patterns in which the stem width is measured
by the distance ratio r(unit)/r(stem). Thus,
instead of increasing the cylindrical radius while adding primordial units with
increasing radii, the cylindrical radius may be frozen while the size of the
units is decreased (see next paragraph). The maximum distance ratio is presumed
to be 1, defining the initial cotyledons, and it diminishes during the stacking
of new spheres. (Just below the apical tip lies a central cell region with
relatively low mitotic activity: the "mother cells" [47] or the mristme
d'attente [43, 48, 49]. This region is accompanied by another
hypodermal one with high mitotic activity in which primordia are initiated
(Buvat's anneau initial). Its
annular shape causes canalization. In flowers such as Ranunculus acris, stamen
and carpel primordia are initiated in a spiral sequence [50].) The stem's
absolute thickening has no topological significance. The settling height for
new spheres depends on the configuration of the upper units.
The place of a new
spherical unit is calculated as if it were the last (top) one to be
constructed. At the very moment of placing the unit, the growth process is
simulated topologically. Thus, the results of arising, developing, and
positioning are copied while at the same time the possibility of stacking more
units on the structure is maintained by its cylindrical shape. This is achieved
by positioning units locally in the correct manner, with their size related not
to each other but to their receptacle. Because in the model the stem is
cylindrical with radius 1, it is easy to calculate correct unit sizes. When
these are known for initiating primordia of any ordinal number, a construction
or even a growth simulation for a certain point in time of development can be
executed. (The stack-and-drag computer program is not only capable of producing
images of the stacking iterations during calculation and the calculation
results, but also shows the growth process from cotyledons to flowering
adults.) To understand the relative sizing in the model, we should imagine the
development on the apical dome as follows (Figure 6): The extreme top of the
apical dome, being a point, is not the growth center; the perimeter of the
cluster of mother cells determines a ring of development. In fact, there can
never be a growth center without dimensions. One should speak rather of an
expanded point.
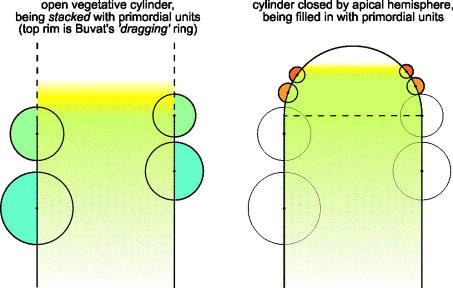
FIG.6. Transition from vegetative to reproductive stage, interpreting
Buvat's concept. Left: A new unit may arise in
the initiation zone (shaded area) when there is no room left between the
neighboring units just below it. A unit may not arise at a position
significantly lower than a preceding unit. The initiation zone has a width that
relates closely to the upper unit sizes. In vegetative structures, represented
in the cylinder stage of the model, the initiation zone is relatively wide. Right:
Determinate growth. The cylinder is closed by an
apical hemisphere, being filled in with primordial units that meet at a point
not necessarily lying exactly on the Z
axis. Unit radii are related to the cylinder radius (see Figure 10).
2.4 The
three S curves
The model makes use
of three S curves [51]: the unit growth curve and two translating curves
simulating axial and radial stem growth. (The vegetative apex promotes
longitudinal growth, and the reproductive apex produces a meristematic envelope
with a large surface area from which the parts of a flower or flowers develop
[52]. The transition from vegetative to reproductive apex is gradual [52].) In
the model, the moment of transition from indeterminate (vegetative) to
determinate growth is preset. In contrast to the number of vegetative units, the
exact number of units that fit on the apical hemisphere is not predictable.
2.5 Differentiation
and the relationships between pattern, shape, and color
Closely connected
with the expansion of a plant structure in radial and axial directions is the
differentiation of primordial parts. (Many characteristics of flowers are
related to the phyllotaxis of floral organs [53].) In general, differentiation
in living structures can be explained by positioning signals [54]. Below, it
will be shown how to get some essential shape and color differentiations as a
by-product after translations. As a consequence, the stack-and-drag model
relates pattern (phyllotaxis), shape (differentiation), and coloring (although
it is not a pertinent variable) to each other.
3 Model
description
The stack-and-drag
model comprises two main processes: (1) creating patterns in which
spheres of different sizes are positioned using the same algorithm throughout
the entire construction and (2) shaping structures in which
the centers of the spheres are translated and the spheres are resized to
simulate axial and radial growth of stem and organs. In the first process a
growth curve defines sphere radii in relation to receptacle radius (Figure 7).
In the second two similar curves define translations in the distinguishable
stem parts. [The S curve is defined by parameters b (minimum),
h (half-life), and c (gradient) as Sn= (1-b) / (1+e c.(h-n)),
in which n is an ordinal number, e =
2.71828... (the Euler number), b is the base or
minimum relative sphere radius, h is half-life or the
ordinal of the sphere of radius 0.5, and c is the growth
constant or gradient. A unit defined as a primordium or sphere of influence
including primordium-forming cells is represented as a sphere with its center
on a cylindrical or hemispherical receptacle with radius 1. Unit radii can be
expressed as Rn = 1- Sn.]
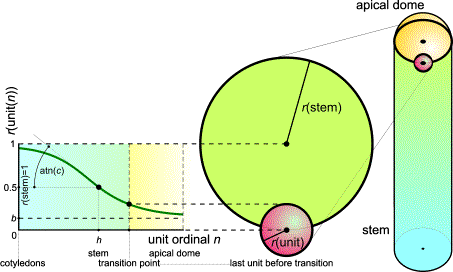
FIG.7. The relation (unit radius)/(stem radius). The unit shown is the
last vegetative one, lying on the cylinder. Unit sizes are defined by the S
curve [53].
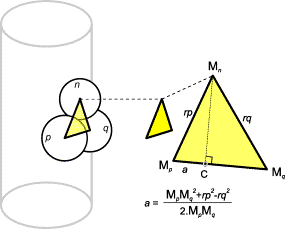
FIG.8. Unit n will have contacts p and q when the previous unit (n -1) had units p -1 and q -1 as its contacts. Unit p lies
counterclockwise around the positive Z
axis against unit n. rp = r(n)+r(p); rq = r(n)+r(q). The center of unit n,
M(n), is the intersection of a circle with center C with the
cylinder. If a neighboring unit intersects unit n, it will replace unit p or q.
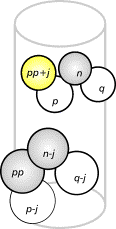
FIG.9. The highlighted unit (pp+j) will
be counted, for unit n-j has unit pp as one of its support units. An increase in j indicates a decrease in sensitivity, for units in lower positions are
counted.
3.1 Creating
patterns
Sizes of spheres as phyllotactic units
are calculated; their centers are situated at distance 1 from the Z axis.
The stacking direction is upwards from two initial touching spheres (Figure 2).
These two spheres, representing cotyledons, have a unit radius of 1. Units are
constructed using positioning algorithms of the dislodgement model (Figure 8).
The main rule is that when unit n lies against the
contacts with ordinal numbers p and q, unit n+1 will
be positioned at the contacts p+1 and q+1. (In
the dislodgement model, checks are needed to trace units as intersecting
candidates [7, 32]. The stack-and-drag model uses some of these checks and
decides which one of the support units has to be dislodged. If p=p(n)
and q=q(n) are the ordinals of the support units
of unit n, then (1) unit p may be replaced by
one of the following units with ordinals p+n-q, q+q-p, p+q-n, p(q)+n-q,
p(p)+n-p, and (2) unit q may be replaced by
one of the units with ordinals q+n-p, p+p-q,
q+p-n, q(p)+n-p, q(q)+n-q.) After the last unit
on the cylindric stem, spheres close the surface in a transition from vertical
to horizontal: the apical hemisphere with unit radius 1 (Figure 4). The
parameters used are (i) tls, number of spheres on the cylinder,
initiating spheres included; (ii) exp, expansion - spheres
can be compressible or repulsive, depending on age; (iii) sens, sensitivity
- the placement of spheres depends on past configurations (Figure 9); and (iv) canal,
canalization - the ring in which a sphere is allowed to be constructed
is chosen narrow to wide (Figure 10). (The expansion factor declines downward
along the receptacle. One of the consequences is that misplacement of units
caused by the static character of unit configurations in the simulation is
neutralized [16]. High sensitivity means that only the locations of the upper
spheres predict the settling of a new sphere. Low sensitivity means that lower
spheres on the cylinder influence the settling of a new sphere. Strong
canalization is caused by a narrow placement zone.)
3.2 Shaping
structures
After forming the
pattern on the receptacle, we displace units in the axial and radial
directions. Translation depends on unit ordinal or age n, but also
on d, the distance to the Z axis, and on z,
the height from the XY plane. Stem growth causes shifting in
the phyllotactic pattern. Translations follow the S curve (Figure 7), being a
function of n but also of z or d, respectively.
Axial translations are expressed as
Axn
= (1-Sn) . znLinkZ
in which zn is
relative height (0 < zn £ 1) and LinkZ causes
displacements to depend on n to zn (0 £
LinkZ £ 10). Parameter LinkZ leaves the
dependence open, for there is no evidence to exclude either n or z. Note
that axial translations and unit sizes use similar graphs when LinkZ = 0.
Radial translations are expressed as
Radn
= Sn . dnLinkD
in which dn is
relative distance (0 < dn £ 1) and LinkD causes
displacements to depend on n to dn (0 £ LinkD
£ 10). Notice that radial translations and unit sizes
use horizontally mirrored graphs when LinkD = 0.
To simulate
flowering according to the catastrophe theory [51], the three curves for unit
growth, axial translations, and radial translations must work closely together.
The distance ratio r(unit)/r(stem) is of
decisive importance here. At the time of inflorescence, high values result in
flowers and low values result in flower heads.
When spherical
units are replaced by stem surface-filling polygons, which reveal vascular
units [55-57], differentiation is simulated. (For defining leaf and internode
as one unit, see also the leaf-skin model and the phytonic model in [39].) To
understand this, we consider a given unit with both of its two support units and
more lower units if necessary (Figure 11). The lower part of the top unit
develops as an appendage, and the top parts of the lower units will contribute
stem-filling parts. The length and top position of the appendage may be changed
by specific parameters that are related to radial or axial translations. The
use of these parameters leads to remarkable results when they are simply
related to unit positions. In this way, differentiation and corresponding
coloring in the distinguishable "plant" parts arise spontaneously,
conditioned by the S curves. Adjacent polygons form a honeycomb structure, as
in pineapple.
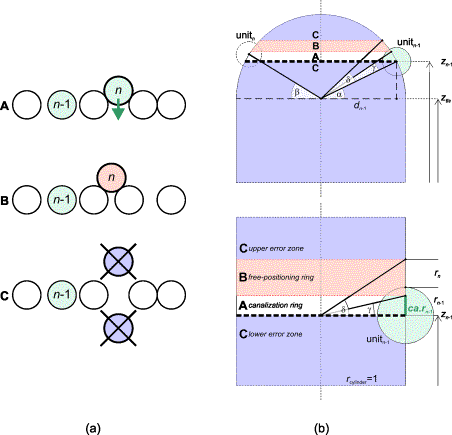
FIG.10. (a) Side view of unrolled
cylinder. A new unit that fits or nearly fits between its predecessors (A, canalization zone) will be part of the existing ring. When it has been
located significantly higher (B, free positioning
zone) due to lack of space below, it will be the first unit in a new ring.
Extreme high or low positions indicate an error (C, upper and lower error zone). (b) Bottom: Vertical section through the cylinder. The upper border of the
canalization ring is settled by ca.r(n-1) or angle g, as well as by z(n-1). Angle d, where tan(d)=[r+r(n-1)]/r(cylinder), determines the upper
border of the free positioning ring. A unit that has been placed within this
ring retains its calculated position. Higher values for ca will narrow the ring. Top: Vertical
section through the hemisphere. Angles a,
where tan(a)=[z(n-1)-z(tls)]/d(n-1),
and b, where tan(b)=[z-z(tls)]/d,
define the ring's shifting. [z is the elevation of unit n; z(n-1) is the elevation of unit n-1;
z(tls) is the elevation of the last vegetative unit; r(n) is the radius of unit n; ca is the canalization factor.]
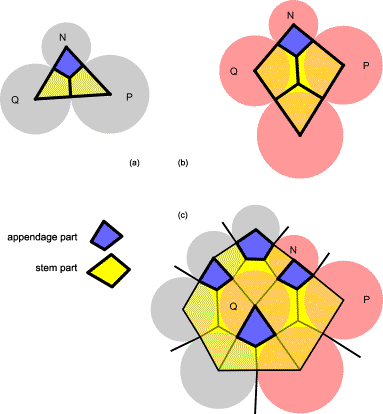
FIG.11. Differentiations by the vascular unit [56]. Primordial shapes
depend on the local configuration of units. (a) Defined by three primordial
units of the model, the vascular unit PQN
shows stem parts (yellow) and an appendage part (blue) [7]. (b) A vascular unit
can, for example, be rhomboid. (c) The vascular unit of (b) is shown here in a
configuration of primordial units in the stack-and-drag model. In this case,
the central primordial unit Q is septagonal.
(Appendage parts are blue.)
4 Results
My earlier
dislodgement model [7] was sufficient for simulations with recognizable
positioning of individual primordia on early flower heads [58].
Variable values for
some vegetative and floral structures have been compared by using the
stack-and-drag model (Table 1 and Figures 12-19) [59, 60]. The computer program
ApexS [59], which generates patterns and structures, is able to produce very
different phyllotactic patterns along the vegetative axis as well as in flowers
and flower heads. Helices appear almost exclusively in Fibonacci numbers (1, 1,
2, 3, 5, 8, 13, ...), and successive units make XY-projected
angles of ~137.5¡, starting from right angles or the decussate arrangement at
the base. Accessory series of the Fibonacci sequence may arise as sudden
anomalies without particular parameter presettings. Canalization, which is
induced by the mechanism as depicted in Figure 10, results in rings of units in
fixed numbers like Fibonacci terms. The preference for fixed numbers in
canalization follows from the preference for these numbers in parastichies. In
contradistinction to stability for fixed numbers in parastichies, units often
show canalization in deviations close to those numbers. (The computer program
ApexS has a size of ~400 kBytes. It runs in the Windows environment of personal
computers.)
Synthetic
phyllotactic shift by gibberellic acid [36] is simulated (see veg/gibb and
Figure 12).
The Lucas sequence
(1, 3, 4, 7, 11, 18,...) is generated under comp/lucas. It is
not directly deducible from the parameter values that Lucas numbers will arise.
Appearance of the numbers is caused by an early stacking accident [9] (Figure
16).
The early
development of the composite flowering head of Microseris pygmaea [19] is
simulated after parameter settings in the Table 1 column comp/micr (Figure
18).
The column cost/costus
shows simulation values for Costus (Costaceae).
Spiromonostichy in the species Costus scaber has been regarded
as an unsolved problem for 120 years [35]. The apical dome is enclosed by
sickle-shaped bract primordia, which show a lower and a simultaneously developing
higher part. The higher part of a given bract overlaps the lower part of a
previous bract. In the terms of our model, two spheres of influence define one
primordium (Figure 19).
TABLE I: Comparison of parameters in the Stack-and-Drag Model for some
structures
|
|
structure |
||||||||||||||
|
|
veg |
|
|
flow |
|
|
|
|
comp |
|
|
|
spike |
cost |
fruit |
|
|
dec |
gibb |
canal |
8532 |
52 |
333 |
1313 |
wild |
lucas |
sun1 |
sun2 |
micr |
mais |
cost |
pinapp |
|
tl |
50 |
40 |
113 |
32 |
24 |
16 |
79 |
142 |
55 |
105 |
5939 |
67 |
311 |
202 |
261 |
|
tls veg |
50 |
40 |
30 |
10 |
10 |
5 |
20 |
100 |
20 |
20 |
80 |
10 |
300 |
200 |
200 |
|
exp |
0.70 |
1.27 |
0.50 |
1.10 |
1.10 |
0.80 |
1.05 |
1.00 |
1.00 |
1.00 |
0.95 |
0.77 |
1.10 |
1.40 |
1.05 |
|
sens |
0.90 |
0.96 |
1.00 |
0.95 |
0.95 |
1.00 |
0.90 |
0.96 |
0.96 |
1.00 |
0.98 |
0.90 |
0.90 |
0.95 |
0.96 |
|
canal |
0 |
0.30 |
1.00 |
0.70 |
0.85 |
0.58 |
0.65 |
0.70 |
0.50 |
0 |
0 |
0.20 |
0.90 |
0 |
0.09 |
|
base |
1.00 |
0.63 |
0.15 |
0.24 |
0.28 |
0.33 |
0.16 |
0.19 |
0.17 |
0.13 |
0.015 |
0.17 |
0.42 |
0.50 |
0.16 |
|
hlife |
0.52 |
0.50 |
0.30 |
0.60 |
0.50 |
0.40 |
0.50 |
0.90 |
0 |
0.50 |
0.44 |
0.80 |
0.05 |
0.15 |
0.05 |
|
const |
0.10 |
-1.22 |
0.17 |
0.49 |
0.69 |
0.69 |
0.34 |
0.22 |
0.22 |
0.27 |
0.07 |
0.27 |
0.17 |
0.10 |
0.34 |
|
see fig |
|
12 |
|
13 |
14a |
14b |
|
15 |
16 |
|
17 |
18 |
|
19 |
|
|
tl |
calculated number of
spheres on the cylinder and the hemisphere |
|
tls veg |
number of spheres to be
constructed on the cylinder |
|
exp (0.5-1.5) |
units are compressible
to repulsive |
|
sens (0-1) |
unit is settled with
feedback with existing structure to strong sensitivity |
|
canal (0-1) |
units are stacked
(leaning on neighbors) to dragged, or pulled (by Buvat's ring) |
|
base (0-1) |
growth function minimum |
|
hlife (0-1...) |
ordinal of unit with 0.5
x stem radius related to tls |
|
const (0-1) |
growth function
steepness |
Notes and remarks:
(1) Only pattern-defining parameters are shown.
(2) hlife may be in excess of 1.
This is due to the definition of hlife as
related to the vegetative number of units.
(3) cont may be negative in
artificial conditions, where the S curve is reversed.
(4) Combinations of pattern-characterizing values are printed in italics.
(5) All patterns have been generated in the same single process. All
structures have been translated, differentiated, and colored in a single
progression. All figures are unedited output of the program ApexS [59] and have
been drawn after a single command. Pattern calculation speed on a PC (Pentium
90) is approximately 150 units/s.
|
veg/dec |
Decussate leaf
positioning with stem torsion caused by the phyllotactic pattern. |
|
veg/gibb |
See Figure 12. |
|
vegl canal |
Strong canalization
leads to distinct whorls with many primordia when the unit constant is kept
small. One of the rings has 16 (doubled Fibonacci number) units. |
|
flow/8532 |
See Figure 13. |
|
flow/52 |
See Figure 14a. |
|
flow/333 |
See Figure 14b. |
|
flow/1313 |
Flower with numeric
canalization 13-13-8-5. Units in a canalized ring may show inequality in form
and function. |
|
flow/wild |
See Figure 15. |
|
comp/lucas |
See Figure 16. |
|
comp/sun1 |
Composite with a low
number of florets. |
|
comp/sun2 |
See Figure 17. |
|
comp/micr |
See Figure 18. |
|
spike/mais |
Grains are in 5 x 2
columns. |
|
cost/costus |
See Figure 19. |
|
fruit/pinapp |
A pineapple is regarded
as a thickened stem. Leaves on the fruit are small, and fruit polygons are
vascular units. |
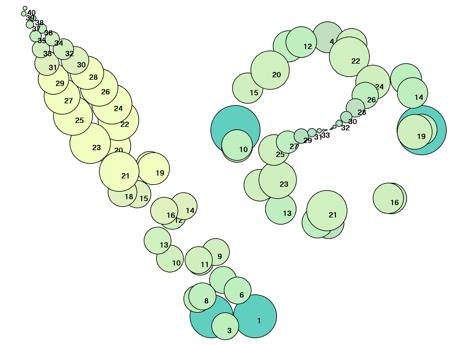
FIG.12. veg/gibb The phyllotactic shift decussate / spiral (Fibonacci) / distichous in Hedera
helix L. after injection with gibberellic acid at the
arising of unit 20 [36]. Right: Top
view of the stacking, with spheres drawn small to show pattern change. Note that
the numbering of primordial spheres does not preclude the possibility of
primordia simultaneously arising in the actual plant (see Section 2.2.).
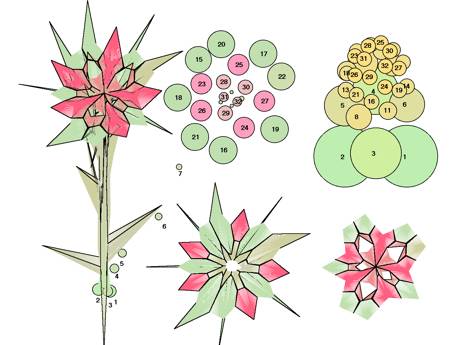
FIG.13. flow/8532 Flower
showing 8-5-3-2 canalization. Strong canalization with high unit constant results
in a simple flower with distinguishable parts. Left: Appendages are expressed by polygons (vascular units with their upper
tips in particular translated by the parameter leaf-length). From bottom left to center top: Spheres
pattern with translated and resized units. Top right: Calculated stacking with 10 spherical units on the cylinder and 21 on
the apical hemisphere (cylinder and hemisphere are not shown). Bottom center
and right: Top view of the flower parts, which
are divided by a horizontal plane between, and caused by, canalization rings.
Note that (1) phyllotaxis is decussate (unit pairs 3+4, 5+6) near the
cotyledons; (2) sepals, petals, and stamens/carpels show a three-way (vascular
unit) division; and (3) in this case the flower is singularly minor
symmetrical.
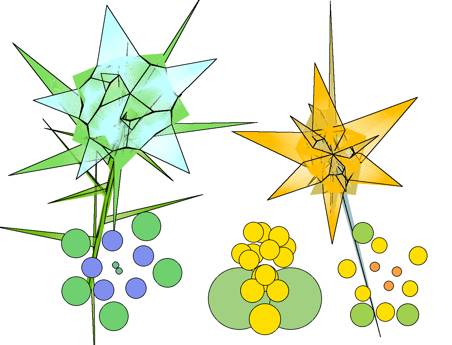
FIG.14. flow/52 and flow/333 Left: 5-2 flower after 10 vegetative units with flower diagram after
translations of the calculated units. Right: 3-3-3
flower after only five stem units (cotyledons included) with a total of 16
units. Bottom: Calculated untranslated
stacking, showing all units. Bottom right: Diagram
showing the dissimilarity of the four whorls of flower parts, although there
may be a six-petal symmetry.

FIG.15. flow/wild Wild phyllotaxis, with very regular flower.
Left: The centers of the contacts (support units) of each
unit are connected, showing (1) a stem pattern transition wild-decussate and
(2) floral canalization. Center: Calculated
stacking, translated spheres, leaves. Right, top to bottom: The vascular units for sepals, petals, stamens, and carpels, divided by
horizontal canalization planes (see also Figure 13).
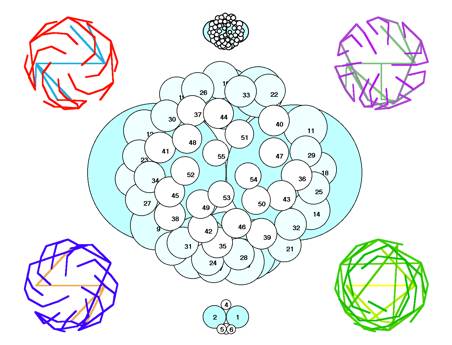
FIG.16. comp/lucas Deviation
of the Fibonacci phyllotaxis [9]. Center, bottom: The early deviation at n=6, which causes
the Lucas phyllotaxis. Center, top: Follow-up
from n=6. Corners: Connections
of centers of units n-p, n-q, n-p(q), p-q.
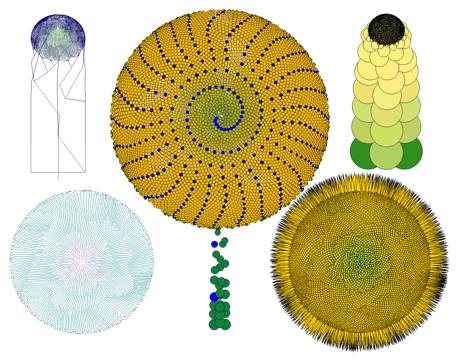
FlG.17. comp/sun2 Composite with a very high number of
florets. Left: Possible vascular pattern:
oblique; untranslated; and top view, translated. Right: Calculated spheres packing and top view of flower head with seeds. Center:
Axial and radial translations, with every 13th unit
highlighted.
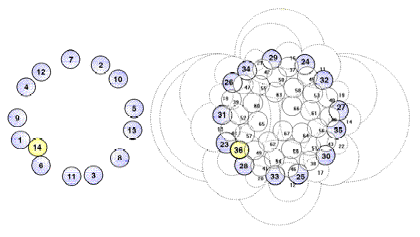
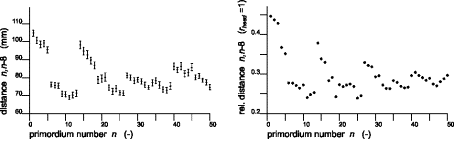
FIG.18. comp/micr Topological/graphical
results. Simulation, compared with observations in flower heads of Microseris
pygmaea D. Don [19]. A special problem is the canalization
jump after the first annular arrangement of 13 primordia. Observations (left)
are compared with simulation results. (Top) Topological: Canalization jump out of the basical capitulum ring with
13 primordia. Left: Model according to
observations [19]. Top right: Computed pattern,
including (highlighted) 13-ring and canalization jump. (Bottom) Graphical: Characteristic patterns in three-dimensional distances
between primordia. Left: Relations according to
observations [19]. Right: Three-dimensional
distances between units n and n-8. Note that (1) distances are dimensioned differently; in the model,
they are related to the (untranslated) cylinder radius; (2) the simulation is
done for an embryonic stage, so (radial) translations are small; and (3) to get
optimal approximations, the simulation is begun by assuming rough values and
fine-tuning is done by a trial-and-error procedure. Once graphs become similar,
the characteristic values of the model parameters are known.
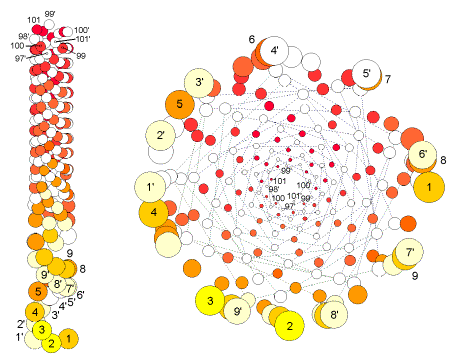
FIG.19. cost/costus Small divergence angles; scarcely translated
structure showing the small torsion as a phyllotactic, not physiologic, quality
in Costus scaber [35]. Left: Because of its embracing sickle shape, a primordium is defined here by
two units. Right: Schematic presentation in
top view, with connections between centers of subsequent units. Note that of
the two near lower units, one is always not a direct contact.
5 Discussion
5.1 The
model
The stack-and-drag model has been
built on three basic size/shape assumptions (Figure 20a-c):
(1) There are three
plant parts: the initiating cotyledons (represented by two spheres), the
vegetative stem (represented by a cylinder), and the generative apex
(represented by a hemisphere).
(2) Plant
appendages are regarded in relation to internodal stem parts. A primordial unit
is always combined with two supporting lower units. Adjoining parts of these
three spheres form the vascular unit [57].
(3) Three interacting
S curves determine the growth of primordia and plant body: one for unit growth,
one for axial expansion, and one for radial expansion.
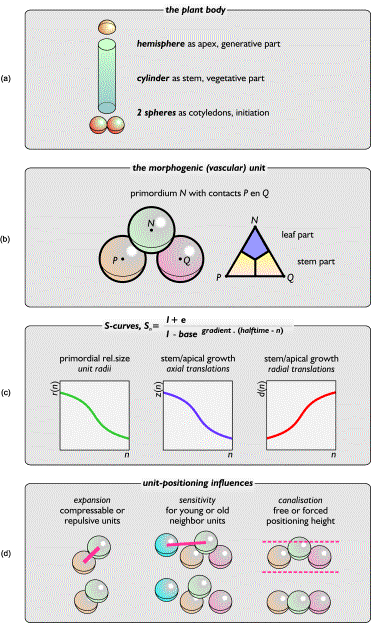
FIG.20. Basics in the stack-and-drag model. (a) The three parts of a
plant reflected by the model. (b) Two spheres P and
Q determine the location of a third sphere, N. Translations determine shape and color of the vascular unit PQN. (c) The unit growth curve (left)
is important for pattern development, and the other curves define the
receptacle's growth. (d) Three pattern-defining parameters simulate different
levels of interaction between units.
5.2 The
parameters
Three parameters
can be isolated to produce a wide range of recognizable phyllotactic patterns: b
determines the minimum relative size of a primordial unit (Figure 7), exp
gives the compressibility of units, and canal is a
measure of the sharpness of the annular dragging zone in which units may arise
(Figure 20d). Three additional parameters are of less importance: h and c
together with b determine the path of the S curve for the size of
early primordial units, and tls is the number of
vegetative units that indirectly defines the unit size just before
inflorescence and the unit growth rate.
5.3 The
drag component
The status of the
drag parameter canal is a moot point. As depicted above, in the small
physical scale of phyllotactic pattern formation we realized the necessity for
a counterpart of gravity, the influence of which diminishes with size. We
interpreted Buvat's embryonal ring as a zone of pressure from the hypodermal
shoot apical meristem on the epidermal layers and combined this with the
assumption that outer layers have to follow after central elongation. The
biological nature of the drag parameter has to be specified.
5.4 Branching
Bud formation is possible by permitting a structure to branch
outside its cylindrical casing. Fractal theories are not satisfactory for
obtaining branching patterns because they lack sufficient biological evidence.
One approach might be to integrate the L-systems [62]. On the other hand, the
fractal property should be a qualification like the angle of 137.5¡ is.
5.5 Phyllotaxis
and differentiation
The stack-and-drag
model tries to reduce the question of the origin of phyllotaxis to the question
of primordial differentiation. What we know about differentiation in a
developing living structure is that, given the potential of any embryonic cell
to specialize in any adult organ function, morphological changes in cell
clusters are strongly directed by chemical diffusion and physical tension from
their environment. The geometrical orientation of cell clusters in their
environment (phyllotaxis) is crucial to the way these influences act upon them
[63]. Phyllotaxis is governed by annular differentiation of the apex, and after
that, the differentiation of primordia is governed by phyllotaxis [17].
We may consider
physical and chemical forces to indirectly shape the shoot apex including the
primordia arising on it. Shape influences differentiations and therefore new
initiating points for primordia. If the shape is known and the influence of
forces is translated into universal geometrical parameters, a continuation of
the process of pattern development can be deduced.
Although the true
character of differentiation is still unknown, we do have knowledge of the
character of the arising phyllotactic patterns. By reducing the number of
parameters to only those that are recognizable geometrical parameters, the
problems of differentiation and phyllotaxis have been disconnected. The a-b-c
model for specification of organ identity in flower development [17, 63]
seems to link up closely with this conclusion and may be useful in the future
development of determinate differentiation in the stack-and-drag model.
I
thank Konrad Bachmann for his push toward the present model and his
proofreading, Johannes Battjes for the feedback from his observations and
interpreting, Roger Jean for the exchange of some opposing thoughts, and the
independent reviewers for their critical comments on the manuscript and
consequent improvements.
References
1 D.
W. Bierhorst, On the stem apex, leaf initiation, and early leaf ontogeny in
filicalean ferns, Am. J. Bot. 64(2):125-152 (1977).
2 P.
B. Green, Surface of the shoot apex: a reinforcement-field theory for phyllotaxis,
J. Cell Sci. Suppl.
2:181-201 (1985).
3 R.
H. Smith and T. Murashige, In vitro development of the isolated shoot apical
meristem of angiosperms, Am. J. Bot. 57:562-568 (1970).
4 S.
Douady and Y. Couder, Phyllotaxis as a physical self-organized growth process, Phys.
Rev. Lett. 68(13):2098-2101 (1992).
5 C.
Goodall, Eigenshape analysis of a cut-grow mapping for triangles, and its
application to phyllotaxis in plants, SIAM J. Appl.
Math. 51(3):775-798 (1991).
6 P.
B. Green, A theory for inflorescence development and flower formation based on
morphological and biophysical analysis in Echeveria, Planta 175:153-169 (1988).
7 F.
M. J. van der Linden, Creating phyllotaxis: the dislodgement model, Math.
Biosci. 100(2):161-199 (1990).
8 L.
A. Bursill and Fan Xudong, Close-packing of growing discs, Mod. Phys. Lett.
B, 2 (11, 12):1245-1252 (1988).
9 P.
K. Endress, Patterns of floral construction in ontogeny and phylogeny, Biol.
J. Linnean Soc. 39:153-175 (1990).
10 W.
A. van Heel, Androecium development in Actinidia chinensis and A. melanandra (Actinidiaceae), Bot.
Jahrb. Syst. 109:17-23 (1987).
11 L. F.
Hernandez and J. H. Palmer, Regeneration of the sunflower capitulum after
cylindrical wounding of the receptacle, Am. J. Bot. 75:1253-1261 (1988).
12 G.
S. Hicks and I. M. Sussex, Development in vitro of excised flower primordia of Nicotiana
tabacum, Can. J. Bot. 7:133-139 (1970).
13 R. V.
Jean, Mathematical Approach to Pattern and Form in Plant Growth, Wiley-Interscience, New York, 1984.
14 G.
J. Mitchison, Phyllotaxis and the Fibonacci series, Science 196:270-275 (1977).
15 R.
F. Williams and E. G. Brittain, A geometric model of phyllotaxis, Aust. J.
Bot. 32:43-72 (1984).
16 J.
Battjes, thesis, Determination of organ numbers during inflorescence
development of Microseris (Asteraceae: Lactuceae)
Amsterdam Univ., 1994, pp. 43, 44, 110-122.
17 E.
S. Coen and E. M. Meyerowitz, The war of the whorls: genetic interactions
controlling flower development, Nature 353:31-37
(1991).
18 I.
Adler, A model of contact pressure in phyllotaxis, J. Theor. Biol. 45:1-79 (1974).
19 J.
Battjes, N. O. E. Vischer, and K. Bachmann, Capitulum phyllotaxis and numerical
canalization in Microseris pygmaea, Am. J. Bot. 80(4):419-428
(1993).
20 A.
H. Church, The principles of phyllotaxis, Ann. Bot. 18:227-243 (1904).
21 R.
Dixon, The mathematical daisy, New Sci. 17:792-795
(1981).
22 M. Hirmer, Zur Kenntnis
der Schraubenstellungen im Pflantzenreich, Planta 14:132-206 (1931).
23 W.
L. Kilmer, On growing pine cones and other Fibonacci fruits - McCulloth's
localized algorithm, Math. Biosci. 11:53-57
(1971).
24 F.
J. Richards, Phyllotaxis: its quantitative expression and relation to growth in
the apex, Phil. Trans. Roy. Soc. Lond. B235:509-564
(1951).
25 P.
H. Richter and R. Schranner, Leaf arrangement: geometry, morphogenesis, and
classification, Naturwissenschaften 65:319-327
(1978).
26 D.
W. Roberts, A contact pressure model for semi-decussate and related
phyllotaxis, J. Theor. Biol. 68:583-597 (1977).
27 J. C. Schoute, Beitrge
zur Blattstellungslehre, Rq. Trav. Bot. Nerl. 10:153-324 (1913).
28 O. Schepp,
Konstruktionen zur Blattstellungstheorie, I, Ber. Deut. Bot. Ges. 41:255-262 (1923).
29 G. Van Iterson, Mathematische
und Microskopisch-Anatomische Studien ber Blattstellungen, Gustav Fischer
Verlag, Jena, 1907.
30 H.
Vogel, A better way to construct the sunflower head, Math. Biosci. 44:179-189 (1979).
31 d'A.
W. Thompson, On Growth and Form, Cambridge
Univ. Press, London, 1917, pp. 759-766.
32 F.
M. J. van der Linden, Phyllotactic patterns for domes, Int. J. Space Struct. 9(1):9-19 (1994).
33 F.
M. J. van der Linden, The dislodgement model improved, in thesis Phyllotactic
Patterns for Domes, I:1-5 (1994).
34 P.
Prusinkiewicz and A. Lindenmayer, The Algorithmic Beauty of Plants, Springer-Verlag, New York, 1990, pp. 99-118.
35 B.
K. Kirchoff and R. Rutishauser, The phyllotaxy of Costus (Costaceae), Bot. Gaz. 151(1):88-105
(1990).
36 J.
Marc and W. P. Hackett, Gibberellin-induced reorganization of spatial relationships
of emerging leaf primordia at the shoot apical meristem in Hedera helix L., Planta 185:171-178 (1991).
37 R.
O. Erickson, The geometry of phyllotaxis, in The Growth and Functioning of
Leaves, J. E. Dale and F. L. Milthorpe, Eds., Cambridge Univ.
Press, New York, 1983, pp. 53-88.
38 R. V.
Jean, A basic theorem on and a fundamental approach to pattern formation on
plants, Math. Biosci. 79(2):127-154 (1986).
39 R.
Rutishauser and R. Sattler, Complementarity and heuristic value of contrasting
models in structural botany 1, Bot. Jahrb. Syst. 107:415-455 (1985).
40 H. S. M.
Coxeter, Regular Polytopes, Dover, New York,
1963.
41 K.
Miyazaki, An Adventure in Multidimensional Space, Wiley, New York, 1986.
42 R.
Williams, The Geometrical Foundation of Natural Structure, Dover, New York, 1979.
43 R.
Buvat, Structure, volution et functionnement du mristme apical de quelques
dicotyldones, Ann. Sci. Nat. Bot. Ser. 11.13:199-300
(1952).
44 W. Hofmeister, Allgemeine
Morphologie der Gewchse, Engelmann, Leipzig, 1868.
45 M.
Snow and R. Snow, On the determination of leaves, New Phytol. 46:5-19 (1947).
46 S.
Schwendener, Mechanische Theorie der Blattstellungen, Leipzig, 1878.
47 R. F.
Lyndon, The shoot apex, in Cell Division in Higher Plants, M. M. Yeoman, Ed., Academic, London, 1976, pp. 285-314.
48 A.
Nougarde, Organisation et functionnement du mristme apical des vgtaux
vasculaires, in Travaux Ddis au Lucien Plantefol, Masson, Paris, 1965.
49 L.
Plantefol, Hlices foliaires, point vgtatif et stle chez les dicotyldones.
La notion d'anneau initial, Rev. Gen. Bot. 54:49-80
(1947).
50 R.
D. Meicenheimer, Relationships between shoot growth and changing phyllotaxy of Ranunculus,
Am. J. Bot. 66(5):557-569
(1979).
51 J.
H. M. Thornley and K. E. Cockshull, A catastrophe model for the switch from
vegetative to reproductive growth in the shoot apex, Ann. Bot. 46:333-341 (1980).
52 W. R.
Philipson, The ontogeny of the shoot apex in dicotyledons, Biol. Rev. 24:21-50 (1949).
53 A. Fahn,
Plant Anatomy, 4th ed., Pergamon, Oxford,
U.K., 1990, pp. 65, 413.
54 L.
Wolpert, The shape of things to come, New Sci. June:38-42
(1992).
55 P. P.
Larson, Development and organization of the primary vascular system in Populus
deltoides according to phyllotaxis, Am. J. Bot. 62:1084-1099 (1975).
56 P.
P. Larson, Vascularization of developing leaves of Gledistsia triacanthos,
Am. J. Bot. 71:1201-1220 (1984).
57 G.
A. Pieters and M. E. Van der Noort, The morphogenic unit: the essence of
morphogenesis, Dept. of Plant Physiol. Research, Agric. Univ. Wageningen, The
Netherlands, manuscript, 1978.
58 J.
Battjes and F. M. J. van der Linden, Positioning of primordia on early flower
heads of Microseris pygmaea: a comparison of
SEMs and simulations by the dislodgement model, unpublished results, 1992.
59 F. M. J.
van der Linden, Results of 'ApexD' and 'ApexS': structures, graphs, tables, in
thesis Phyllotactic Patterns for Domes, IV:1-39 (1994).
60 F. M. J.
van der Linden, Creating phyllotaxis from seed to flower, in Symmetry in Plants,
R. V. Jean and D. Barab, Eds., World Sci. Publ.,
Singapore, 1998, 19:487-521.
61 F. M. J.
van der Linden, Computer program 'ApexS': key algorithms, in thesis
Phyllotactic Patterns for Domes, II:1-29 (1994).
62 A.
Lindenmayer, Development algorithms: lineage versus interactive control
mechanisms, in Development Order: Its Origins and Regulation, S. Subtelny and P. B. Green, Eds., Alan R. Liss, New York, 1982, pp.
219-245.
63 J.
Helsop-Harrison, Sex expression in flowering plants, Brookhaven Symp. Biol. 16:109-125 (1964).